Research
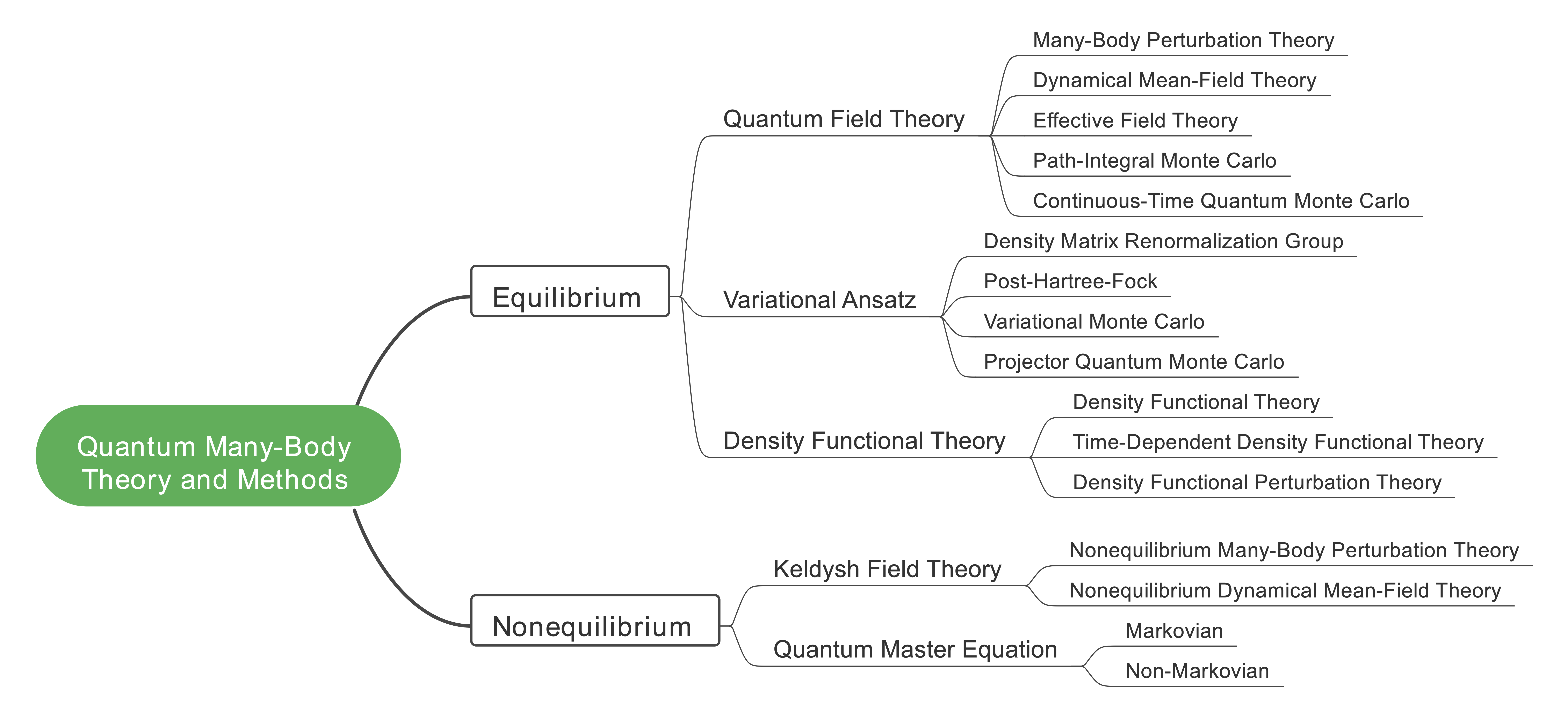
Quantum Many-Body Theory and Methods
- Quantum many-body physics is principally a complicated problem with high complexity, where emergent phenomena are hidden behind strong correlations beyond the mean-field. I am broadly interested in mathematical structure of quantum many-body physics. With the mathematical formulation well-understood, reasonable approximations can be made, useful information can be kept for the emergent phenomena of interest, and even predictions can be made in a way of first-principles.
- In quantum field theory, the quantum many-body problem is formulated as a many-body action with infinite degrees of freedom, with which the physical quantities of interest can always be expressed. By diagrammatic expansion and truncation obeying the conservation laws, reasonable approximations can be made in a controlled manner. Famous examples include the Hartree-Fock approximation, the GW approximation and the dynamical mean-field approximation etc. These approximations can be equivalently found in many-body perturbation theory (MBPT) and dynamical mean-field theory (DMFT). These approaches can also be combined together, that is the so-called quantum embedding, with which the strongly correlated region of the system can be specially treated. Keldysh formalism together with non-equilibrium Green's function (NEGF) extends field theory to the non-equilibrium regime, which enables the study of out of equilbirum phenomena such as quantum transport.
- Different from field theory, the quantum many-body problem can also be approached in a wave function perspective, with which the expectation value of a physical quantities of interest can be calculated. Formly, the true many-body wave function can be expanded as an infinite series of Slater determinants with infinite orders. In quantum chemistry, the series are truncated according to command, and the approximate expansion coefficients are obtained by diagonalization; in quantum Monte Carlo (QMC), the true ground state is represented by an imaginary-time evolution of a trial wavefunction, which can be computed with stochastic sampling; in density matrix renormalization group (DMRG), the quantum state or narrowly the ground state wave function is represented by a matrix product state (MPS) where the correlation is reserved, and the variation is achieved by iterative optimization of each tensor block with the matrix product operator (MPO). Density matrix embedding theory (DMET) can be viewed as a simplified but cheaper version of DMRG.
- Density functional theory (DFT) is a self-contained theory based on electron density, which provides a good mean-field starting point of electronic structure in most cases.
- Open quantum system represents a big class of problems where a small system, whose reduced quantum dynamics is of interest, is interacting with a big environment. The evolution of the system can be obtained by tracing out the environment degrees of freedom from the total density matrix. In the Markovian approximation, the standard procedure yields the Lindbald quantum master equation; in the non-Markovian case, introducing the projection operator yields the Nakajima-Zwanzig quantum master equation.
- As a PhD student at UChicago, I am focusing on deriving and developing quantum defect embedding theory (QDET) which is a natural framework for the description of strongly correlated many-body states of promising spin-defects for quantum information science. As an intern student at Flatiron, I am focusing on application of discrete Lehmann representation (DLR) which is a compact representation of imaginary-time Green's functions, to Green's function theories including DMFT and MBPT for acceleration of real calculations.
- Besides, I also have research experience in development of DMRG algorithm for quantum chemistry, two- and four-component approaches for relativistic quantum chemistry, as well as a non-Markovian and non-perturbative quantum master equation approach, that is the hierarchical equations of motion (HEOM), for quantum dynamics simulation.
Quantum Computation and Simulation
- Due to the exponential complexity of quantum many-body physics, naturally it is unfavorable to simulate quantum with classical computers. On the contrary, the promising quantum computers, which hold the same nature of quantum, provide unlimited possiblities. For this reason, I am also interested in algorithms for simulations on quantum computers.
- In general, quantum computers have great advantage in memory due to the way of encoding. Quantum computers have also been proved to be powerful in time dependent simulations. No explicit proof has been established for the scaling of state related simulations on quantum computers so far.
- In the current noisy intermediate-scale quantum era (NISQ), quantum phase estimation (QPE) is still not feasible and variational quantum eigensolver (VQE) is often adopted as the solver for an effective physical Hamiltonian of interest. However, the results from VQE is typically severely corrupted by the noise from the current quantum architechture. In order to reduce the error from the perspective of a theorist, what we can do is to design post-processing error mitigation scheme for this purpose.
- Quantum computers can also be a good host for QMC calculations. Specifically, efficient algorithms can be designed for controlling the fermionic sign problem on quantum computers.
- Last but importantly, the current NISQ quantum computers provide a rough many-body wavefunction, which could be used as starting point in many cases.
Numerical Analysis and Scientific Computing
- Including but not limited to quantum, I am broadly intereted in numerical analysis, scientific computing as well as the related software development. In many cases, physical problems, especially those are limited by computational cost, can be investigated in a mathematical way and from that angle, robust numerical tricks as well as fast algorithms can be introduced to identify and solve the bottleneck. Furthermore, the structure of software can often be designed and optimized for the target.
- Quantum mechanics is defined on an inifinite dimensional Hilbert space, the operations on which can be explained as matrix transformations. For this reason, numerical algorithms in matrix theory such as Lanczos algorithm, Schmidt decomposition, singular value decomposition, QR decoposition and randomized singular value decomposition etc are useful and powerful. Differently, the schoedinger equation indicates that quantum can also be approached from a PDE perspective, where the solution can be obtained from PDE solver. Also, the tensor formalism, i.e. the tensor network methods, can also be used to represent the high-dimensional correlation within the many-body wavefunction.
- Depending on the quantum representation, optimization algorithms such as steepest descent, least squares, and those based on properties of convex functions, e.g. semidefinite programming, can be developed and utilized to obtain the physical quantities of interest, e.g. the ground state wavefunction, with possible combination with Monte Carlo. In many cases, e.g. QMC sampling, the calculations are almost independent from each other and can be implemented in a heavily parallel fashion using MPI or GPU.
- As a graduate student at UChicago, I am developing tensor network methods and Monte Carlo methods for the committor function, which is the solution of a backward Kolmogorov equation for a rare event and ground state properties of quantum many-body systems. I am a developer of open source software WEST (Without Empty States) for large scale MBPT calculations, and the main developer for QDET. As an intern student at Flatiron, I participate in the development of open source software TRIQS (Toolbox for Research on Interacting Quantum Systems) for DMFT calculations.
